There is an inherent beauty to be found in simple, pervasive ideas that shift our perspective on familiar objects. Such ideas can help tame the complexity of abstruse abstractions by offering a more intuitive angle from which to understand them.

The aim of this post is to present an alternative angle — that of interactive semantics — from which to view one of the fundamental notion of functional programming: higher-order functions.

Interactive semantics provide an intuitive understanding of the concept of higher-order functions, which is a worthy mathematical investigation in itself. But this approach is also practical, shedding a new light on existing programming techniques and programming language features. We will review the example of higher-order contracts in this post. We will also present direct application of interactive semantics in the design and the implementation of programming languages.

Denotational semantics

Take the following programs, written respectively in Java, Rust, and Haskell:

public int incrByTwo(int x) {
  return x + 2;
}

fn incr_by_two(x: i32) -> i32 {
    let constant = 1;
    let offset = 1;
    constant + offset + x
}

incrByTwo :: Int -> Int
incrByTwo x = 1 + x + 1

While they look different on the surface, our intuition tells us that they are also somehow all the same. But what does “being the same” even mean for functions defined in such different languages?

One point of view is that syntax is merely a way to represent a more fundamental object, and that each of the above examples in fact represents the exact same object. From a purely mathematical point of view, these programs all fundamentally represent the function which adds $2$ to its argument.

$f : \mathbb{Z} \to \mathbb{Z} = x \mapsto x + 2$.

The process of stripping away the purely syntactic details of a program to discover the mathematical objects at its core is the main concern of the field of denotational semantics. We refer to the mathematical object a program represents as its denotation. The idea being that by ridding ourselves of the unimportant details of a particular syntax we can focus better on the essence of the program.

The motivation for doing this partly stems from fundamental philosophical questions, such as: “what really is a program?” Attempting to answer such questions unveils deep connections between computer science and the rest of mathematics. However, stripping a program down to its substance can also provide us with techniques to answer much more concrete questions. For example: proving that two given programs always behave in the same way.

While incrByTwo operates on integers, even the most bare-bone functional language features much more complex objects: functions.

Higher-orderness

A higher-order function is a function which manipulates other functions. The various instances of incrByTwo only represent a first-order function, since their sole argument is a number. On the other hand, the usual map operation on lists is higher-order, as it takes as an argument a function describing how to transform each element of the list. This can be seen clearly in the Haskell syntax for the type of map, in particular the presence of the function type (a -> b) as the first argument:

map :: (a -> b) -> [a] -> [b]

Integers are easy to grok. They are static pieces of data that one can inspect and pass around. Functions are a different matter: they are an opaque entity that can only be actioned by handing it over data or functions.

This distinction is not only theoretical but also practical: while choosing a concrete representation of integers on a CPU is often relatively simple, selecting a representation for functions and closures, together with a calling convention, is not.

Traditionally, mathematicians have simply encoded functions as data. In set theory, the formal lingua franca of modern mathematics, a function is a (potentially infinite) set of tuples pairing each input with the corresponding output. Our incrByTwo denotation $n \mapsto n+2$ is represented as the infinite set:

$\{\ldots, (-1, 1), (0,2), (1,3), \ldots \} = \{ (n, n+2) \mid n \in \mathbb{Z} \}$

While the set representation of functions is useful for mathematics, a static, infinite dictionary with virtually instant lookup turns out not to be a great model for computation, for a number of philosophical and technical reasons¹. At its core, the notion of functions as sets ignores a fundamental concept of computation: time, and its direct manifestation, interaction.

Interactive semantics

Game Semantics (GS hereafter) is a line of thought which takes its root in dialectical interpretations of logic. In GS, we not only consider the inputs and outputs of a higher-function, but also all the interactions with other functions given as arguments. That is, we consider the traces of the function (the Player in GS), viewed as a dialogue with an Opponent, representing the environment in which the function executes (the calling context).

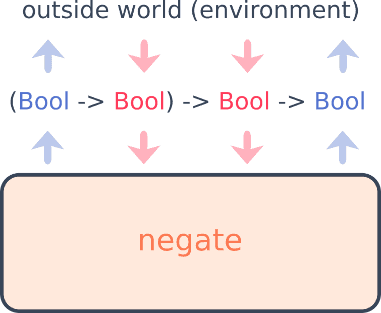
Take a simple higher-order function:

negate :: (Bool -> Bool) -> Bool -> Bool
negate f x = if f x then false else true

The evaluation of the run negate (\y. y) false now corresponds to a play in a game defined by the type of negate. Let’s first attach a unique label to each occurrence of Bool:

(Bool -> Bool) -> Bool -> Bool
( B1 ->   B2 ) ->  B3  ->  B4

The play goes like this ²:

• Opponent (caller): hey, could you give me your return value (B4) ?
• Player (negate): sure, but first give me the return value of f (evaluating f x, B2)
• O: ok, but first give the value of its parameter y (B1)
• P: ok, then I need the value of my parameter x (B3)
• O: x is false (B3)
• P: then y is false (B1)
• O: then f returns false (B2)
• P: then I finally return true (B4)

The full denotation of negate is then a strategy for this game.

Polarity

The game partitions the occurrences of Bool into outputs/positive, where the Opponent asks first and the Player answers, and inputs/negative, where roles are switched. This distinction is called polarity.

Consider the anonymous function \y. y from the previous call to negate (let’s call it f).

The play for f false, from the point of view of f, looks like:

• O: asks for return value
• P (f): asks for parameter y
• O: answers y is false
• P: returns false

If you come back to the first play of negate and hide the moves external to the call f x, the above play exactly matches a subset of the original one, just with the polarities flipped!

• Opponent (caller): hey, could you give me your return value (B4) ?
• Player (negate): sure, but first give me the return value of f (evaluating f x, B2)
• O: sure, but first give the value of the its parameter y (B1)
• P: ok, then I need the value of my parameter x (B3)
• O: x is false (B3)
• P: then y is false (B1)
• O: then f returns false (B2)
• P: then I finally return true (B4)

The Player/Opponent distinction is perfectly symmetric. Indeed, from the point of view of f in the subcall f x, the caller is negate, which thus becomes the opponent.

Determining the polarity is easy: look at the type of the function and compute the path from the root to a type occurrence in terms of going to the left or to the right of an arrow. The occurrence is positive if the number of left is even (including 0), and negative otherwise. For negate, working on a type with labels and parentheses ((B1 ->a B2) ->b (B3->c B4)):

• B1 is positive (left of ->b, left of ->a)
• B2 is negative (left of ->b, right of ->a)
• B3 is negative (right of ->b, left of ->c)
• B4 is positive (right of ->b, right of ->c)

The essence of GS is to model the execution of a higher-order function as an interaction over basic values. The beauty lies in the simplicity of the concept and the perfect symmetry between Player and Opponent. Polarity tells us if a value is an input, which must be provided by the environment, or an output, which must be provided by the function, either directly or indirectly through subcalls.

From a theoretical perspective, GS was the first technique to provide a class of denotational models that satisfy a strong form of correspondence between programs and their denotations (they gave the first fully abstract model for PCF). Game semantics seems to hit a sweet-spot by hiding unessential aspects of programs without forgetting the essential dynamic of interaction.

But the GS point of view is also practical. Let’s illustrate a few applications equipped with our new interactive lens.

Applications

Higher-order contracts

At Tweag, I am working on a configuration language called Nickel. Nickel features contracts, a form of higher-order dynamic type-checking. Contracts enable safe interaction between typed code and untyped code by preventing the untyped code from injecting ill-typed parameters.

Take a variant of our negate function in Nickel:

let negate : (Bool -> Bool) -> Bool -> Bool = fun f x => !(f x)

When calling e.g. negate (fun y => y) false from untyped code, the interpreter will check that the values bound to x, y, f x, and !(f x) are booleans.

Now, if we break the contract of f by calling negate (fun y => 2) false, the first line of the output will be:

error: contract broken by the caller

Conversely, if we define negate to break the contract of f³:

negate | (Bool -> Bool) -> Bool -> Bool = fun f x => !(f 5)

And make a legal call negate (fun y => y) false, the error becomes:

error: contract broken by a function

Higher-order contracts are precisely exploiting the same idea of breaking higher-orderness into first-order interactions! A contract for a higher-order function decomposes into primitive contracts (here Bool), incurring one check for each type occurrence. The blame distinction caller/function corresponds to the polarity of GS.

The trace of the second example looks like (labelling the type as (B1 -> B2) -> B3 -> B4):

• Opponent (caller): let’s check that negate returns a Bool (evaluating negate (fun y => y) false, B4)
• Player (negate): sure, but first let’s check that f returns a Bool (evaluating f x, B2)
• O: ok, but then I need a Bool for y (B1)
• P: ok, then I need a Bool for x (B3)
• O: x is false (B3)
• P: ok, false is a Bool. Then y is 5 (B1)
• O: hey, 5 is not a Bool! I blame the player (B1)

For the typed version of negate, Player represents the internal, type-safe boundaries. Opponent is the external world, potentially untyped, and the contract is the border police meticulously controlling everything that crosses the boundary.

Circuits and distributed computing

If you look at the plays of the previous section, they have strong feeling of message-passing style. The function is exchanging primitive data with the environment. This view has been exploited for example to design compilation techniques and a language runtime that makes it trivial to break down terms and run them on distinct distributed nodes. In contrast, making a classic stack-based virtual machine distributed is not trivial.

The interactive interpretation has been used as well to compile high level functional programs down to integrated circuit, precisely by reducing the complexity of higher-orderness to exchanging first-order messages⁴.

Conclusion

Interactive semantics like Game Semantics have moved forward the understanding of the nature of programs and computations by incorporating an aspect forgotten by a naive set-based semantics: interaction. Such interactive semantics have proven theoretically fruitful and particularly flexible (they can model side effects, concurrency, and more). Game Semantics also has practical applications by serving as a guideline for compilation techniques and language design.

But in the end, I think that the richness of the interactive semantics resides in its surprisingly simple and intuitive foundation (who has never played games!). My humble hope for this post is that in a no so distant future, you may stare at a language feature, an abstract concept or a programming technique and suddenly exclaim:

Of course! It’s just that higher-orderness is first-order interaction.