In Property Based Testing (PBT) the programmer specifies desirable properties or invariants for the code under test, and uses a test framework to generate random inputs to find counter-examples. For example, “a reversed list has the same size as the original list” which can be written as:

fun l -> List.length (List.reverse l) = List.length l

Imagine this test fails for the list [42; 9079086709; -148; 9; -9876543210]. Does this counter-example fail the test because there are 5 elements? Or because there are negative numbers? Or maybe due to the big numbers? Many reasons are possible.

To help narrow down the cause of test failures, most PBT libraries provide a feature called shrinking. The idea is that once a test fails for a given input, the test engine will try less complex inputs, to find a minimal counter-example. In the example above, if shrinking reduces the minimal failing input to [-1] then the developer will more quickly find the root cause: most likely a problem with negative numbers.

This post discusses a type of shrinking called integrated shrinking in OCaml — this feature has recently been merged into QCheck, and will appear in QCheck2.

Shrinking in QCheck1

In QCheck1, the type of an arbitrary (used to generate and shrink input values) is equivalent to:

type 'a arbitrary = {
  generate : Random.State.t -> 'a;
  shrink : 'a -> ('a -> unit) -> unit
}

• generate is used to generate random values
• shrink is used in case of test failure to find a smaller counter-example

If the second argument of shrink is unsettling, you can simply read it as “the test to run again on smaller values”. For example, to aggressively shrink (try all smaller numbers) on an int, one could implement shrink as such:

let shrink bigger run_test =
  for smaller = 0 to bigger -- 1 do
    run_test smaller
  done

For convenience, it is never mandatory in QCheck1 to provide a shrinking function: the shrink field is therefore an option. By default, no shrinking is done.

Problems with manual shrinking

There are several problems with the QCheck1 approach, which we will refer to as manual shrinking.

Invariants

Many generators enforce some invariants, meaning that shrinking must also ensure these invariants. For example, a generator of numbers between 10 and 20, in case of test failure, must not try numbers lower than 10! In practice this usually means duplicating the invariant code in generate and shrink. This repetition is tedious and creates a risk of introducing a discrepancy between the generator and the shrinker, causing shrinking to be unreliable.

Providing shrinking is optional

Because providing the shrinking function is optional to run a QCheck1 test, in practice developers forget or don’t take time to implement it for each generator. As a consequence, when a test fails, developers either need to interrupt their work flow to implement all missing shrinkers, or try to identify the problem without shrinking. Either way, the developer is slowed down.

Feedback loop and return on investment

Writing PBT generators requires investing a bit more work up-front than unit tests, but this investment pays off a few minutes later when you write and run your tests.

In contrast, writing shrinking code up-front can feel frustrating as it might not provide a benefit soon, or at all. This frustration is usually worsened by the fact that most shrinking code looks the same:

• shrinking a product type (record or tuple) amounts to calling the shrinking functions of each field in sequence
• shrinking a sum type amounts to pattern matching and then calling the shrinking function of the inner value

QCheck1 arbitraries don’t compose well

As shown above, an arbitrary is a pair of a generator — a function that produces values — and a shrinker — a function that consumes values. As such, it is invariant. This makes composition hard, often even impossible: e.g. if you have an 'a arbitrary and a function 'a -> 'b, it is impossible to obtain a 'b arbitrary while maintaining shrinking:

type 'a arbitrary = {
  generate : Random.State.t -> 'a;
  shrink : 'a -> ('a -> unit) -> unit
}

let map (f : 'a -> 'b) ({generate = generate_a; shrink = shrink_a} : 'a arbitrary) : 'b arbitrary =
  let generate_b random = f (generate_a random) in
  let shrink_b bigger_b run_test_b = shrink_a ??? (fun smaller_a -> run_test_b (f smaller_a)) in
  in {generate = generate_b; shrink = shrink_b}

Notice the ??? placeholder: its type is 'a, but all we have at our disposal is f : 'a -> 'b and bigger_b : 'b. Starting from a value of type 'b is is therefore impossible to generate a value of type 'a here.

In QCheck1, map takes an optional reverse function ~rev:'b -> 'a to fill that ??? placeholder and thus maintain shrinking, but all the problems listed above remain. Also, not all functions can be reversed: e.g. consider the function is_even : int -> bool. Once you have a bool, you can’t get back the original int.

Enter Integrated Shrinking

Rather than having a pair of generator and shrinker, integrated shrinking (a kind of automated shrinking) bakes shrinking directly into the generation process: whenever we generate a value, we also generate its shrunk values, and the shrunk values of those shrunk values, etc. This design is directly inspired by Hedgehog. This effectively gives a tree of values:

type 'a tree = Tree of 'a * 'a tree Seq.t

type 'a arbitrary = Random.State.t -> 'a tree

• A tree is a root (a single value) and a (lazy) list of sub-trees of shrunk values
• An arbitrary is a function that takes a random generator and returns a tree

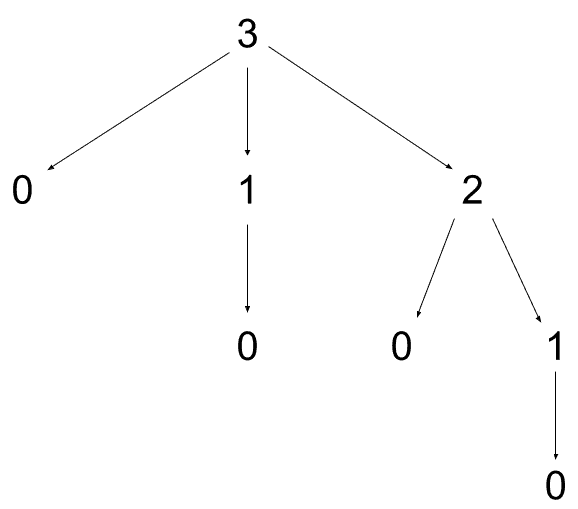
For example, an int arbitrary may generate such a tree:

Notice the use of Seq.t (lazy list) rather than list (strict list): it is unnecessary to generate a shrunk value until it is needed during shrinking.

Consider the (obviously wrong) property “all integers are even”, which can be written in OCaml as fun i -> i mod 2 = 0. Let’s see what happens when this property test runs and the generated integer tree is the one above:

1. the arbitrary function is called with a random state to generate a tree of values (the one above)
2. the tree root 3 is used to call the test, and fails (3 is not even)
3. we now want to shrink 3 to find a smaller counter-example that also fails
4. the property is tested against the first shrink 0 of 3, and the test succeeds: 0 is not a counter-example, so it is ignored
5. the property is tested against the second shrink 1 of 3, and the test fails: 1 is a (smaller) counter-example!
6. the property is tested against the first shrink 0 of 1, and the test succeeds: 0 is not a counter-example, so it is ignored
7. 1 has no other shrunk value, thus 1 is the smallest counter-example we could find: it is reported to the user

Composing arbitraries

Unlike manual shrinking, integrated shrinking does not consume values, it only produces values. Hence integrated shrinking is covariant (while manual shrinking is invariant). This innocuous difference is what makes integrated shrinking better at composition: e.g. it is now possible to implement the map function from above in QCheck2!

type 'a tree = Tree of 'a * 'a tree Seq.t

type 'a arbitrary = Random.State.t -> 'a tree

let rec map_tree (f : 'a -> 'b) (tree_a : 'a tree) : 'b tree =
  let Tree (root_a, shrinks_a) = tree_a in
  let root_b = f root_a in
  let shrinks_b = Seq.map (fun subtree_a -> map_tree f subtree_a) shrinks_a in
  Tree (root_b, shrinks_b)

let map (f : 'a -> 'b) (generate_a : 'a arbitrary) : 'b arbitrary = fun random ->
  let tree_a = generate_a random in
  map_tree f tree_a

The map_tree function maps f over an 'a tree by mapping f on the root value, and recursively mapping f on all its sub-trees. Then map takes care of wrapping up the function over the random state, and delegates to map_tree.

Caveats

Integrated shrinking is not an absolute improvement over manual shrinking: it comes with limitations. I present below some caveats: you can find a more thorough comparison with manual shrinking on Edsko de Vries’s blog post.

Monotonicity

Integrated shrinking (and in particular, the implementation of composition functions like map, bind, etc.) assumes that all composed functions are monotonically non-decreasing, i.e. that smaller inputs will give smaller outputs. In practice, this is true the vast majority of the time, so this assumption is not too constraining. As a counter-example, consider mapping is_even over a generator of numbers. is_even is not monotonic, no matter the order we decide for true and false: e.g. consider the order true < false: 0 < 1 < 2 but is_even 0 < is_even 1 > is_even 2. Indeed while 3 -> 2 -> 1 -> 0 is a good shrinking of the input, mapping is_even over this shrink tree gives false -> true -> false -> true which is a bad shrinking tree. In that case, it does not make sense to rely on an int arbitrary to build a bool arbitrary.

Shrinking strategy for Algebraic Data Types

Shrinking product types (records and tuples) can be done using various strategies. For example, for a record {a; b} one can:

• completely shrink the first value before the second (completely shrink a, and then completely shrink b)
• interleave shrinking of the first and second values (shrink a bit a, then shrink a bit b, then shrink again a bit a, then b, etc.)
• shrink fields together (shrink both a and b at the same time)
• etc.

Similarly, shrinking for sum types (variants) can be done using various strategies. For example, for a variant type A of int | B of string one can:

• consider A smaller than B, thus B shrinks to A before shrinking on the inner string, and A only shrinks on the inner int
• consider neither A nor B is smaller, thus A only shrinks on the inner int, and B only shrinks on the inner string, but shrinking never “jumps” to another variant
• etc.

For both product and sum types, no strategy is better than the others. QCheck2 arbitrarily uses the first strategy in each case, which may not be efficient or even desirable. As for monotonicity, in practice this is rarely undesirable.

Finer control over shrinking

To either change the shrinking strategy, or switch to manual shrinking, QCheck2 provides a lower-level API:

val make_primitive : gen : (Random.State.t -> 'a) -> shrink : ('a -> 'a Seq.t) -> 'a arbitrary

Notice how close this is to QCheck1 arbitrary type (except the shrink function no longer needs to call run_test).

Conclusion

While integrated shrinking is not strictly better than manual shrinking (or other kinds of shrinking), my experience is that its benefits largely outweigh its shortcomings. I am thrilled this was merged, and for once I am looking forward to my next failing test!

I want to give a shout out to Simon Cruanes, author and maintainer of QCheck, for his tight collaboration on Integrated Shrinking, from design to review!