State machines are a common abstraction in computer science. They can be used to represent and implement stateful processes.

My interest in them stems from Domain-Driven Design and software architecture. With this blog post I’d like to explain why I think that state machines are a great tool to express and implement the domain logic of applications.

Moreover, I’d like to present crem, a new Haskell library to build state machines, and explain why Haskell plays an important role in making crem special.

The origin: Domain-Driven Design and state machines

If you are familiar with Domain Driven Design, and Event Storming in particular, you have probably already seen the following picture:

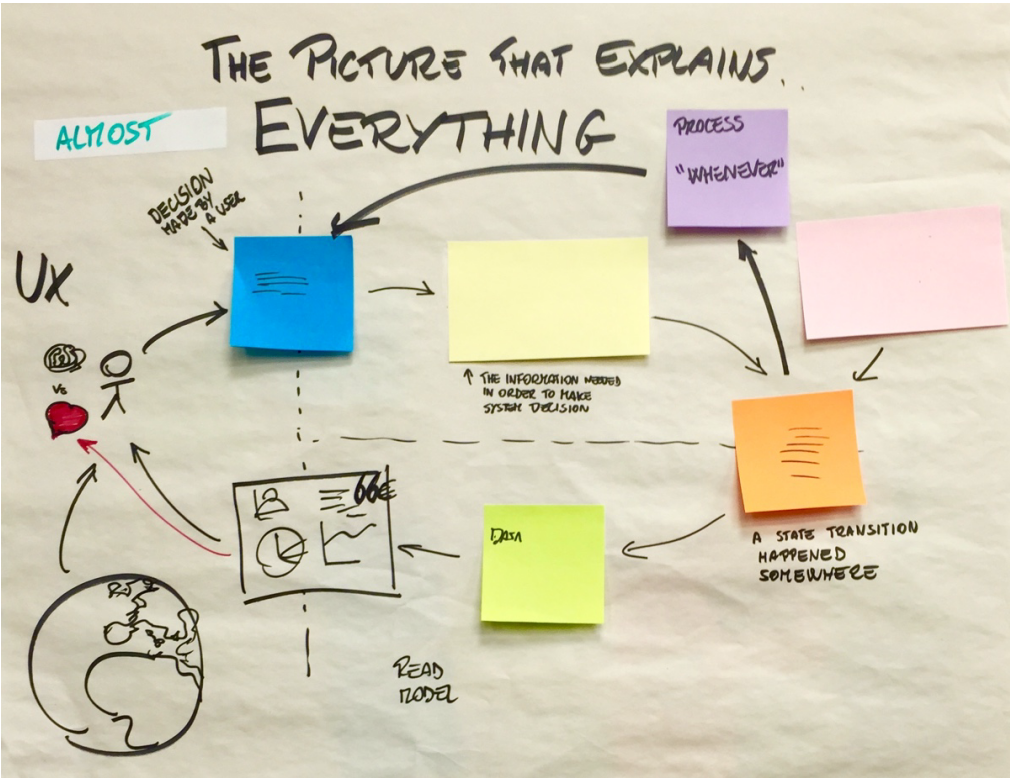
What I always liked about it is that it not only explains the meaning and the role of the different sticky note colours to be used during the Event Storming workshop, but it also hints at a certain style of software architecture. Ideas like CQRS and Event Sourcing play a strong (if not essential) role in such systems.

As I explained in more detail in this blog post, we can view the above picture as a diagram composed of three stateful processes:

• aggregates (the yellow stickies) receive commands (the blue stickies) and emit events (the orange stickies). They are the most important part of your domain logic, where the invariants of your system are checked.

• projections (the green stickies) propagate the information contained in the events to the read models (i.e. the version of your domain model optimized for reading, in a CQRS architecture), which can then be queried by the users.

• policies (the purple stickies), also known as sagas or process managers, describe the reactive logic of a system (whenever ... happens, then do ...). They receive events as inputs and emit commands.

These three process together can fully describe an application domain. Therefore, finding a good way to encode those stateful processes could be extremely beneficial when implementing the domain of your project.

As you might suspect from the introduction, I will argue that state machines are in fact what we are looking for here. There are two main motivations for this:

• State machines are compositional, meaning that it is easy to combine multiple machines into more complex ones. This allows working locally on smaller components, and only when those are ready, combining them into more complex artefacts.

• State machines admit a graphical representation, which really help when documenting and discussing their intended or current behaviour.

How do we model state machines?

If we are to use state machine to encode components of our application domain, we then need a good data structure to encode state machines so that we can leverage their theoretical advantages (compositionality and representability).

If you take a look at the classical definition of a Mealy machine, it is easy to translate it into a Haskell data type like the following:

data Mealy state input output = Mealy
  { initialState :: state
  , action :: state -> input -> (state, output)
  }

The type variables state, input and output are respectively the types of the possible states, the available inputs and the outputs of the machine. initialState is, unsurprisingly, the value of its initial state, of type state. The action function describes how to compute the output and the next state, given the input and the current state.

Machines

If you search for a Mealy data type in the Haskell ecosystem, you’ll stumble across the machines library. Their definition is as follows:

newtype Mealy input output = Mealy
  { runMealy :: input -> (output, Mealy input output) }

It says that, given an input, the machine will produce an output and a new machine, which can then be used in future iterations. The unfoldMealy function allows us to go from the previous version with the explicit state to this one.

The main difference with respect to our previous definition is that now we don’t have a type variable to describe the state space. This means that to retrieve any information about the current state, we will have to pass that as part of the output. On the other hand, this version makes composition much easier, and in fact this new Mealy type is an instance of Category, Profunctor, Strong, Choice and many more which we would not be able to implement for the first version.

These type classes grant us access to sequential composition:

(.) :: Mealy b c -> Mealy a b -> Mealy a c

parallel composition:

(***) :: Mealy a b -> Mealy c d -> Mealy (a, c) (b, d)

and alternative composition:

(+++) :: Mealy a b -> Mealy c d -> Mealy (Either a c) (Either b d)

Such a data type is great for compositionality. On the other hand, once we build a Mealy machine, there is nothing else we can do but run it. The only way to extract information on its internals is to run it. In particular, we lose the theoretical ability to generate a graphical representation of the machine itself.

Recovering a graphical representation

For a given state machine we can define a directed graph of the allowed transitions, where we have a vertex for every possible state, and an edge from a state a to a state b if there is an input which moves the machine from state a to state b. We will call such a graph the Topology of the machine.

What we would like to do is to add the Topology to the definition of a machine. This would grant us two benefits.

• It allows us to check whether a transition is valid.
• It allows us to extract it and use it to produce the graphical representation of the machine we are after.

Since we are working with Haskell, we can ask ourselves whether we want to track such information at the type or at the value level. Storing it at the value level would make it easier to retrieve, but it forces us to check whether a transition is allowed at runtime, and therefore deal with a potential failure. On the other hand, storing such information at the type level allows us to get a compilation error every time someone tries to implement an invalid transition! And, given we are in Haskell, there are techniques to demote type-level information to the value level so that it can be processed there.

Hence, we can strengthen our type to something like:

data Machine
  (topology :: Topology vertex)
  input
  output

where the topology is added among the type variables.

At this point, to define a machine, we first need to define a topology.

$( singletons
    [d|
      exampleTopology :: Topology ExampleVertex
      exampleTopology = _
      |]
 )

We are using the singletons library, so that we can lift the exampleTopology value to the ExampleTopology type, and later on demote the ExampleTopology type back to the exampleTopology value.

At this point, we can define a machine, indexing it with our ExampleTopology type:

exampleMachine :: Machine ExampleTopology ExampleInput ExampleOutput
exampleMachine = _

Too much type-level information makes compositionality harder

The combined usage of the Topology at the type level and of the singletons library allows us to extract information about the defined machines, specifically their allowed transitions, without running the machine.

Still, storing the Topology at the type level makes compositionality harder. Consider, for example, sequential composition:

(.)
  :: Machine topology1 b c
  -> Machine topology2 a b
  -> Machine ??? a c

What should the topology of the result be? Even if we know the answer, this poses two concrete issues:

• We need to compute the resulting topology out of topology1 and topology2 at the type level. This is way more complex than doing it at the value level.
• The presence of the additional type variable prevents us from implementing a Category instance. Similarly, we need to renounce many other useful type classes.

Is there a way to get the best of both worlds; the ability to easily compose our machines and, at the same time, to extract information without running them?

We wouldn’t be here if the answer was no 😊

The best of both worlds

The first thing we need to observe, if we want to achieve our goal, is that having an additional type parameter was making things more complicated with respect to composition. Hence, we start by defining a type with only the input and output type variables:

data StateMachine input output where

With this approach, it looks like we’re losing the Topology information that we tried to add at the type level. In fact, not all is lost, and we can get access to that information by adding a constructor which requires a Machine topology input output:

data StateMachine input output where
  Basic
    :: Machine topology input output
    -> StateMachine input output

We are basically saying that we can construct a StateMachine just by providing a Machine. It looks like we are somehow forgetting information while we do this. In fact, thanks to pattern matching, we can still access the Machine argument and its topology information!

foo :: StateMachine input output -> a
foo stateMachine = case stateMachine of
  Basic machine -> _ -- here we can use `machine`
                     -- and its type-level topology information

Now we need to address compositionality for StateMachine. The trick we can use is add ad-hoc constructors, one for every composition operation that we want to allow:

data StateMachine input output where
  ...
  Sequential
    :: StateMachine a b
    -> StateMachine b c
    -> StateMachine a c
  Parallel
    :: StateMachine a b
    -> StateMachine c d
    -> StateMachine (a, c) (b, d)
  Alternative
    :: StateMachine a b
    -> StateMachine c d
    -> StateMachine (Either a c) (Either b d)

At this point we can easily implement infix operators:

(.) :: StateMachine b c -> StateMachine a b -> StateMachine a c
(.) = flip Sequential

(***) :: StateMachine a b -> StateMachine c d -> StateMachine (a, c) (b, d)
(***) = Parallel

(+++) :: StateMachine a b -> StateMachine c d -> StateMachine (Either a c) (Either b d)
(+++) = Alternative

and enjoy all the compositionality we dreamed of.

Thanks to this encoding, now the responsibility of combining state machines with different topologies is shifted away from the constructors of StateMachine, which are now nicely compositional, to the eliminators of a machine, like running or rendering it.

Generating a visual representation of the state space

A generic term of type StateMachine a b will be a binary tree where every leaf contains a Machine topology x y and every other node corresponds to one of the other constructors, generating a tree like the following:

At this point, we can collect all the information that we have at every node:

• In the leaves we can access the information stored in the topology at the type level.
• In the other nodes, we know how we are composing the subtrees of machines, and we can recursively generate a representation for the subtrees. This is enough to know how to create some interesting representations of the whole machine.

For example, given a machine definition implementing the Domain-Driven Design architecture explained at the beginning of the post, we can generate a diagram representing the flow of the machine:

It clearly highlights the components the whole machine is built from and, for each one of them, it represents its topology (the only non-trivial one is the aggregate).

Crem

The ideas which I’ve discussed in this blog post have been packaged in the crem library.

As discussed above, it allows creating state machines in a compositional way, executing them and generating graphical representations of the state space and the flow of the machines.

Moreover, it contains an abundant level of documentation, many examples, including a DDD inspired application and a terminal-based adventure game, and a cool Nix flake setup for local development.

Conclusion

Wrapping up, the main message of this post is that state machines are a nice abstraction which can be used in extremely practical settings to model and structure our applications. They can be composed easily, and they admit a graphical language to describe and understand them. crem is my attempt at implementing a solution which both preserves these theoretical properties and makes use of them to make your code easier and more maintainable.

Still, crem is in its early stages and I would very much appreciate it if you tried it out and let me know what you think and how it could be improved in any possible way, from its documentation to the nitty-gritty code details.

As a closing note, I’d like to thank all my colleagues who contributed to crem and helped me to shape and polish it.